Das Geflecht von Raum und Zeit – Die Begriffe der Speziellen Relativitätstheorie einfach erklärt

This text will be made available in English soon.

Dieser Text beinhaltet weiterführende Informationen zu meinem Gast-Blogpost Das Rätsel der Zeit, Relativität und Raumzeit, der am 16.12.2024 auf dem Wissenschaftsblog „Natur des Glaubens“ von Michael Blume veröffentlicht wurde.

Er bietet eine allgemeinverständliche Einführung in die wichtigsten Begriffe und Konzepte zur Speziellen Relativitätstheorie.

Lichtstrahlen

Die Elektrodynamik von James Clerk Maxwell (1831–1879) brachte eine erstaunliche Erkenntnis: Elektrische und magnetische Felder können sich als elektromagnetische Wellen frei durch den Raum bewegen. Maxwell zeigte zudem, dass die Geschwindigkeit dieser Wellen mit der Lichtgeschwindigkeit übereinstimmt – Licht ist eine elektromagnetische Welle. Doch diese Entdeckung warf eine wichtige Frage auf: In welchem „Medium“ breiten sich diese Wellen aus? Wasserwellen benötigen Wasser, Schallwellen Luft – aber was ist das Trägermedium für elektromagnetische Wellen?

Wissenschaftler vermuteten zunächst ein hypothetisches Medium, den sogenannten Äther. Zahlreiche Experimente – insbesondere das berühmte Michelson-Morley-Experiment von 1887 – konnten jedoch keinen Äther nachweisen. Diese Ergebnisse stellten die Idee eines Trägermediums infrage.

Albert Einstein (1879–1955) griff diese Frage auf, indem er das Relativitätsprinzip auf elektromagnetische Wellen anwandte. Dieses Prinzip besagt, dass die Gesetze der Physik in allen Inertialsystemen – das sind Systeme, die sich mit gleichförmiger Geschwindigkeit bewegen – gleich sein müssen. Daraus folgt eine erstaunliche Konsequenz: Die Lichtgeschwindigkeit ist in jedem Inertialsystem gleich, unabhängig von der Bewegung der Lichtquelle oder des Beobachters.

Diese Idee war der Ausgangspunkt für Albert Einsteins spezielle Relativitätstheorie. Sie erforderte ein radikales Umdenken in unserem Verständnis von Raum und Zeit.

Die Konstanz der Lichtgeschwindigkeit

Das Michelson-Morley-Experiment lieferte einen der wichtigsten Belege für die Konstanz der Lichtgeschwindigkeit. Die Physiker Albert A. Michelson und Edward W. Morley wollten überprüfen, ob die Bewegung der Erde durch den Äther die Lichtgeschwindigkeit beeinflusst. Dazu konstruierten sie ein empfindliches Interferometer, das kleinste Geschwindigkeitsunterschiede im Licht hätte nachweisen können. (1)

Das Ergebnis war überraschend: Die Lichtgeschwindigkeit blieb stets gleich, unabhängig von der Bewegungsrichtung der Erde. Dieses „Nullergebnis“ widerlegte die Äther-Hypothese und unterstützte die Annahme, dass die Lichtgeschwindigkeit im Vakuum eine universelle Konstante ist – unabhängig davon, wie sich die Lichtquelle oder der Beobachter bewegen.

Raumzeit, Weltlinien und Lichtkegel

Einsteins Erkenntnis über die Lichtgeschwindigkeit führte dazu, dass Raum und Zeit nicht mehr als voneinander unabhängige Größen betrachtet werden konnten. Stattdessen bilden sie eine Einheit: die Raumzeit. Diese vierdimensionale Struktur umfasst drei Raumdimensionen und eine Zeitdimension und beschreibt, wo und wann Ereignisse im Universum stattfinden.

Im Raum-Zeit-Diagramm (2) kann man die Koordinaten von Ereignissen in der vierdimensionalen Raumzeit darstellen.

In der Raumzeit werden Ereignisse durch Raum- und Zeitkoordinaten beschrieben, z. B. „ein Blitz schlägt an einem bestimmten Ort und zu einer bestimmten Zeit ein“. Der Verlauf eines Objekts durch die Raumzeit – all seine Ereignisse – wird als Weltlinie bezeichnet. (3) (4)

• Ein ruhendes Objekt bleibt immer am selben Ort. Seine Weltlinie ist eine vertikale Linie, da es sich nur in der Zeit bewegt.
• Ein bewegtes Objekt, etwa eine Rakete, hat eine geneigte Weltlinie, deren Steigung von der Geschwindigkeit abhängt.
• Die Weltlinien von Objekten, die sich mit Lichtgeschwindigkeit bewegen, wie beispielsweise Photonen, verlaufen im Raum-Zeit-Diagramm auf Geraden, die um 45° gegenüber der Zeitachse geneigt sind.

Im Raum-Zeit-Diagramm kann man alle Ereignisse, die kausal miteinander verbunden sind, durch Lichtkegel darstellen: (5)

• Ereignisse im oberen Lichtkegel können vom Ursprungsereignis in der Zukunft beeinflusst werden.
• Ereignisse im unteren Lichtkegel liegen in der Vergangenheit und könnten das Ursprungsereignis beeinflusst haben.
• Ereignisse außerhalb des Lichtkegels können nicht in kausaler Beziehung stehen, da sich nichts schneller als das Licht bewegen kann.

Diese Lichtkegel legen fest, welche Ereignisse in der Raumzeit durch physikalische Signale oder Bewegungen miteinander verknüpft sein können.

Uhren und Gleichzeitigkeit

Die Konstanz der Lichtgeschwindigkeit zwingt uns dazu, unser Verständnis von Zeit und Gleichzeitigkeit zu überdenken. Traditionell stellen wir uns Gleichzeitigkeit als absoluten Begriff vor: Zwei Ereignisse passieren gleichzeitig, unabhängig davon, wer sie beobachtet. Doch Einsteins Theorie zeigt, dass dies nicht stimmt.

Synchronisation von Uhren

Um Zeit zu messen, braucht man Uhren, die synchronisiert sind. Über Zeit können wir nur dann quantitativ sprechen wenn wir diese auch messen können. Als Uhr können wir uns in diesem Zusammenhang zunächst jedes Gerät oder auch jeden Vorgang in der Natur mit einer periodischen Änderung vorstellen, beispielsweise Energieübergänge in Atomen. Wie aber können wir Uhren miteinander synchronisieren?

Ein einfaches Gedankenexperiment dazu ist die Lichtuhr: Zwischen zwei Spiegeln wird ein Lichtstrahl hin- und her reflektiert. Die Zeit, die das Licht für eine Hin- und Rückbewegung benötigt, definiert den Takt der Uhr.

Relativität der Gleichzeitigkeit

Die Frage, welche Ereignisse gleichzeitig passieren, hängt vom Bewegungszustand des Beobachters ab. Im Raum-Zeit-Diagramm entsprechen gleichzeitige Ereignisse Geraden parallel zur Raumachse (x-Achse). Für einen bewegten Beobachter sind diese Geraden jedoch geneigt. Das bedeutet:

Was für einen Beobachter gleichzeitig ist, kann für einen anderen Beobachter nicht gleichzeitig sein.

Um das zu zeigen, schauen wir uns eine Variante des Lichtuhr-Gedankenexperiments an (folgendes Diagramm). (6)

Zum Zeitpunkt $t_1$ wird im ruhenden System ein Lichtpuls in unterschiedliche Richtungen zu zwei sich jeweils gegenüber liegenden Spiegeln gesendet. Die Weltlinie des Lichtpulses liegt auf Geraden, die um $+45°$ oder $-45°$ Grad gegenüber der Zeitachse geneigt sind. Jede Hin- und Rückbewegung des Lichts entspricht einem „Ticken“ der Uhr.

Wenn die Spiegel das Licht gleichzeitig reflektieren, dann kommen beide Lichtpulse zur selben Zeit wieder an dem Ort an, an dem sie ausgesendet wurden. Im Diagramm unten ist diese Situation für einen unbewegten Beobachter dargestellt, und die beiden Spiegel repräsentieren gleichzeitig stattfindende Ereignisse. Gleichzeitig stattfindende Ereignisse liegen auf Geraden parallel zur x-Achse.

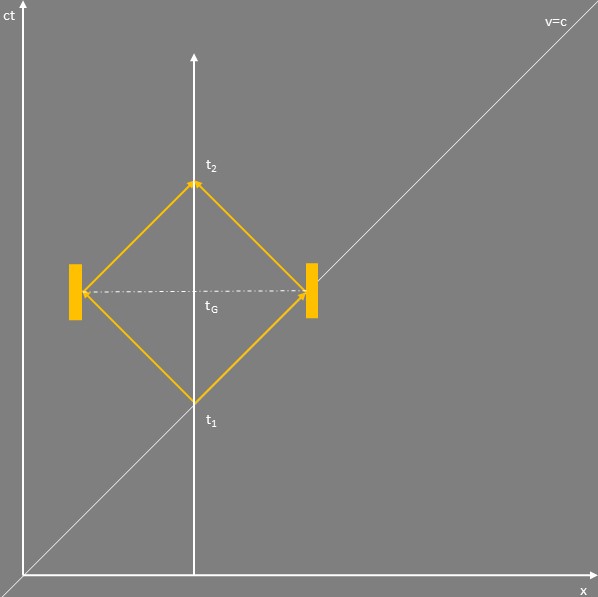
Wie sieht dies nun aus der Perspektive eines bewegten Beobachters aus? Im folgenden Diagramm ist so eine Situation dargestellt.

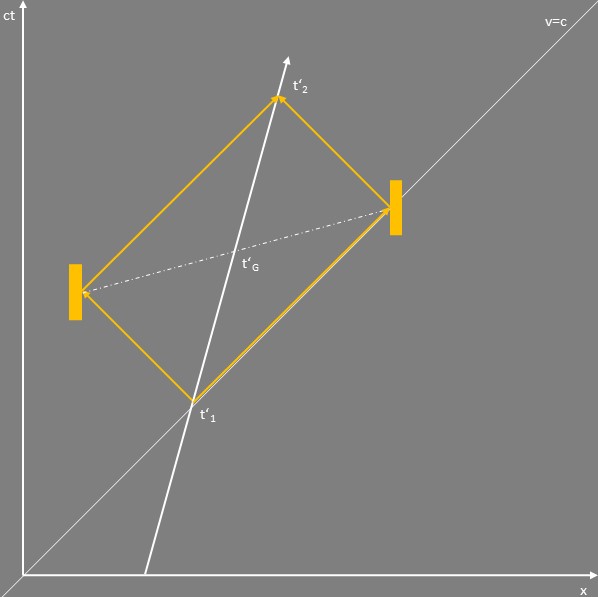
Die Weltlinie des bewegten Beobachters ist gegenüber der Zeitachse gekippt. Man erkennt sofort, dass dieser Beobachter ganz andere Ereignisse als gleichzeitig wahrnimmt als der ruhende Beobachter – nämlich genau solche, für die sich die Lichtlaufzeiten des nach links und des nach rechts ausgesandten Lichtpulses so addieren, dass die reflektierten Lichtpulse zum selben Zeitpunkt $t‘_2$ beim Beobachter ankommen. Die Gerade der für den bewegten Beobachter gleichzeitig stattfindenden Ereignisse ist gegenüber der für den ruhenden Beobachter gleichzeitig stattfindenden Ereignisse geneigt. (7)

Lorentz-Transformation

Gleichzeitig stattfindende Ereignisse in einem Bezugssystem liegen immer auf einer Geraden, die parallel zur x-Achse (im ruhenden Bezugssystem) verläuft. Im Bezugssystem eines bewegten Beobachters sind die Geraden der Gleichzeitigkeit im Minkowski-Diagramm gegenüber der x-Achse geneigt, da sich die Definition von Gleichzeitigkeit mit der Relativgeschwindigkeit ändert. Diese Geraden können genutzt werden, um die x'-Achse eines Koordinatensystems für den bewegten Beobachter im Minkowski-Diagramm zu konstruieren: Sie repräsentiert alle Punkte, die im bewegten System zur Zeit $t' = 0$ gleichzeitig sind.

Ein zentrales Merkmal der Lorentz-Transformation ist, dass die Weltlinien von Lichtstrahlen im Minkowski-Diagramm unabhängig vom Inertialsystem immer unter einem 45°-Winkel verlaufen. Dies folgt direkt aus der Konstanz der Lichtgeschwindigkeit, die durch die Lorentz-Transformation gewährleistet wird.

Die Zeitachse ct' erhält man, indem man eine Linie konstruiert, die in der Minkowski-Metrik orthogonal zur x'-Achse steht. Beide Achsen, x' und ct', sind symmetrisch zur Lichtgeraden geneigt, die die Ausbreitung von Licht darstellt.

Genau diese Transformation, welche die Achsen eines Bezugssystems relativ zu einem anderen neu definiert, ist die sogenannte Lorentz-Transformation, benannt nach dem niederländischen Physiker Hendrik Antoon Lorentz. Sie beschreibt mathematisch, wie sich die Raum- und Zeitkoordinaten zwischen zwei relativ zueinander bewegten Bezugssystemen verändern. (8) (9)

In der speziellen Relativitätstheorie untersucht man Vorgänge in unterschiedlichen Inertialsystemen – Bezugssystemen, die sich mit konstanter Geschwindigkeit relativ zueinander bewegen. Mit der Lorentz-Transformation kann man die Koordinaten von Ereignissen in der Raumzeit zwischen Inertialsystemen umrechnen.

Im Gegensatz zur klassischen Galilei-Transformation berücksichtigt die Lorentz-Transformation die Konstanz der Lichtgeschwindigkeit in allen Inertialsystemen.

Zur Veranschaulichung: Bei der klassischen Galilei-Transformation wird angenommen, dass sich zwei Bezugssysteme mit einer Geschwindigkeit v relativ zueinander in x-Richtung bewegen. In diesem Fall transformieren sich die x-Koordinaten nach der Formel $x→x+vt$, wobei t die Zeit ist. Die Lichtgeschwindigkeit spielt dabei keine Rolle. Die Lorentz-Transformation hingegen stellt sicher, dass die Lichtgeschwindigkeit c in allen Inertialsystemen gleich bleibt. Dies führt zu einer grundlegenden Änderung der Transformationsgesetze und hat tiefgreifende Konsequenzen für unser Verständnis von Raum und Zeit.

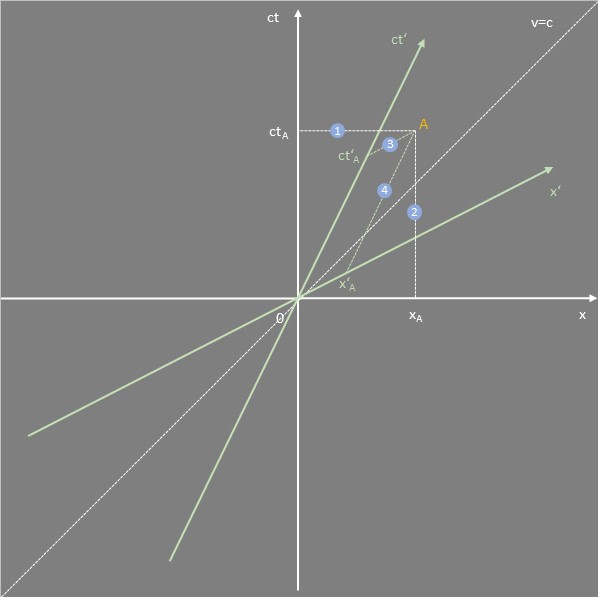
Als Beispiel betrachten wir ein Minkowski-Diagramm, in dem ein Objekt (z. B. Annas Rakete) mit halber Lichtgeschwindigkeit ($v=0,5c$) relativ zum ruhenden Bezugssystem S bewegt wird:

• Die Weltlinie der Rakete verläuft entlang einer Geraden, deren Steigung durch das Verhältnis $v/c$ bestimmt ist.
• Im Ruhesystem der Rakete liegt die Zeitachse ct′ auf der Geraden ihrer Bewegung. Ereignisse, die für die Rakete gleichzeitig auftreten ($t′=0$), liegen auf ihrer x′-Achse.

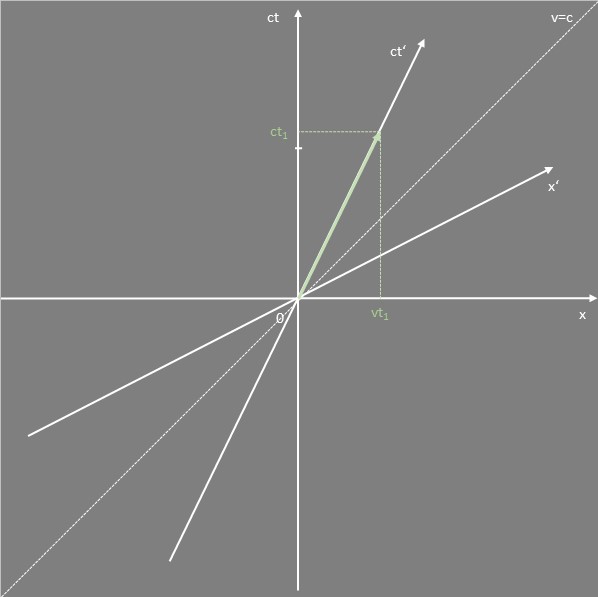
Die Konstruktion der x′-Achse kann geometrisch erfolgen. (10)

Das Diagramm zeigt also die Transformation zweier Bezugssysteme, bei der das System S′ mit halber Lichtgeschwindigkeit ($v=0,5c$) relativ zum ruhenden System S bewegt wird. Der Winkel zwischen den Achsen (x, t und x′, t′) ergibt sich aus der Geschwindigkeit v/c. Für $v=c$ beträgt dieser Winkel 45°, und die x′- und t′-Achse fallen mit der Lichtstrahlgeraden zusammen. (11)

Einheitslängen und Hyperbelgeometrie

Eine interessante Eigenschaft der Lorentz-Transformation ist, dass die Einheitslängen der Achsen (x, x′, t, t′) sich hyperbolisch verzerren. Je näher v an c heranreicht, desto stärker strecken sich diese Einheitslängen entlang der Achsen und gehen asymptotisch gegen unendlich. Dies kann geometrisch durch Hyperbeln im Minkowski-Diagramm dargestellt werden. Raum- und Zeitkoordinaten werden gemäß einer hyperbolischen Geometrie verzerrt, wobei der Raum-Zeit-Abstand (siehe weiter unten) invariant bleibt.

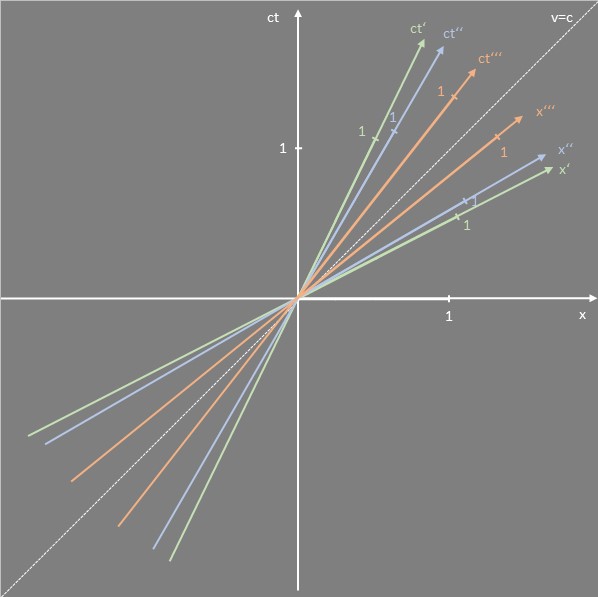
In folgendem Diagramm sind die Orts- und Zeitachsen für drei Inertialsysteme, die sich jeweils mit 0.5c, 0.6c und 0.8c gegenüber dem ruhenden System bewegen, eingezeichnet. Geometrische Betrachtungen führen letztlich zu dem Ergebnis, dass die Einheitslängen der x-, x‘-, x‘‘, und x‘‘‘-Achsen (und entsprechend der Zeitachsen) für die unterschiedlichen Bezugssysteme auf Hyperbeln liegen und asymptotisch gegen Unendlich gehen, wenn v sich c annähert.

Raum-Zeit-Abstand und Eigenzeit

In der speziellen Relativitätstheorie gibt es eine fundamentale, für alle Bezugssysteme invariante Größe: den Raum-Zeit-Abstand oder das Linienelement, gegeben durch:

$d s^2 = c^2 d t^2 - (d x^2 + d y^2 + d z^2)$

Dieser Ausdruck ist analog zum Satz des Pythagoras, jedoch erweitert auf die vierdimensionale Raumzeit.

Über diese Größe kann man die infinitesimale Eigenzeit $d\tau$ definieren:

$c^2 d \tau^2= ds^2$

Das Integral über $d \tau$ entlang der gesamten Weltlinie eines Objekts ergibt die gesamte Eigenzeit:

$\tau =\frac{1}{c}\int \mathrm{d}s$

Die Eigenzeit hat eine zentrale Bedeutung in der Relativitätstheorie: Sie ist die Zeitspanne, die entlang einer Weltlinie gemessen wird, wie sie von einer mitbewegten Uhr wahrgenommen wird. Sie bleibt invariant, unabhängig vom Bewegungszustand des Beobachters, und stellt im Fall einer geraden Weltlinie die kürzeste Zeitspanne zwischen zwei Ereignissen dar.

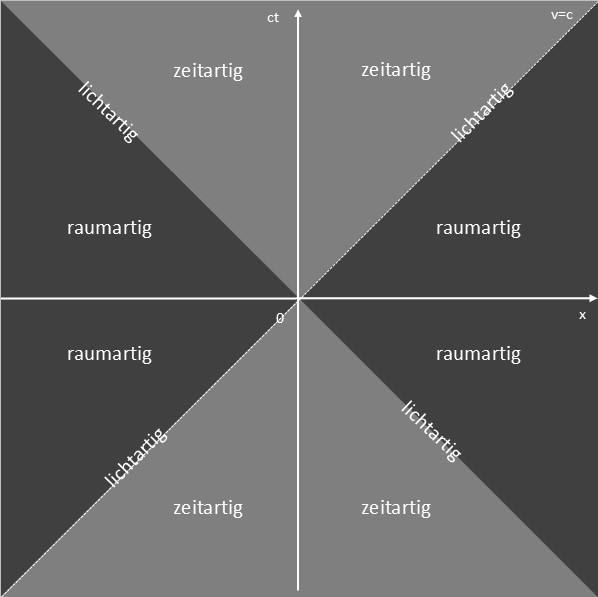
Es lässt sich ein interessanter Zusammenhang zu den Bereichen im Minkowski-Diagramm herstellen:

$s^2 > 0$ beschreibt zeitartige Ereignisse. Es dominiert der Zeitanteil $c^2dt^2$ und die Ereignisse liegen innerhalb des Lichtkegels, können also kausal miteinander verbunden sein. In diesem Fall ist die Eigenzeit eine reelle Größe und gibt die Zeit an, die ein Objekt entlang einer zeitartigen Weltlinie verbringt.

$s^2 = 0$ beschreibt lichtartige Ereignisse. Ereignisse liegen auf dem Lichtkegel und können nur durch Teilchen, die sich mit Lichtgeschwindigkeit bewegen, kausal miteinander verbunden sein. In diesem Fall ist die Eigenzeit gleich 0, was für masselose Teilchen wie Photonen gilt. Für Lichtpartikel vergeht keine Zeit.

$s^2 < 0$ beschreibt raumartige Ereignisse. Es dominiert der räumliche Anteil und die Ereignisse liegen außerhalb des Lichtkegels, können kausal also in keiner Beziehung zueinander stehen. In diesem Fall ist die Eigenzeit eine imaginäre Größe, was bedeutet, dass keine physikalische Eigenzeit zwischen den Ereignissen existiert. (12)

Zeitdilatation und Eigenzeit

Ein Beobachter misst für ein bewegtes System eine längere Zeitspanne ($\Delta t$) als die Eigenzeit ($\Delta \tau$), die im Ruhesystem des bewegten Objekts gemessen wird. Dieser Effekt der Zeitdilatation ergibt sich direkt aus der Lorentz-Transformation (siehe auch diese Quelle):

$\Delta t = \gamma \Delta t'$

Hierbei ist $\gamma$ der Lorentz-Faktor:

$\gamma = 1 \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}$

Der Lorentz-Faktor ist größer als 1. Das bedeutet, dass eine Uhr in einem bewegten System aus Sicht eines ruhenden Beobachters langsamer läuft.

Alle physikalischen Prozesse, wie atomare oder physiologische Vorgänge, verlaufen in Bezug auf die Eigenzeit innerhalb desselben Bezugssystems mit der gleichen Rate. Ein Beobachter kann in seinem eigenen Bezugssystem nicht feststellen, ob seine Uhr langsamer tickt als eine Uhr in einem anderen Bezugssystem. Unterschiede in der Zeitmessung können nur festgestellt werden, wenn Uhren aus verschiedenen Bezugssystemen verglichen werden, etwa durch Lichtsignalvergleiche oder Rückkehrmanöver.

Blockuniversum

Ich möchte noch einen anderen Aspekt der Raumzeit hervorheben. Wir haben ausführlich darüber gesprochen, dass in der Relativitätstheorie Raum und Zeit nicht getrennt behandelt werden, sondern zusammen ein untrennbares Geflecht bilden.

In der Relativitätstheorie existiert die gesamte Raumzeit – Vergangenheit, Gegenwart und Zukunft – als unveränderliches vierdimensionales Gebilde. Ereignisse, die für einen Beobachter gleichzeitig erscheinen, können für einen anderen nicht gleichzeitig sein. Diese Vorstellung führt zum Konzept des Blockuniversums, in dem Zeit nicht fließt, sondern als feste Dimension existiert.

Vergangenheit, Gegenwart und Zukunft sind in diesem Modell relativ und hängen vom Bewegungszustand des Beobachters ab. Unser Eindruck des Zeitflusses ist demnach eine subjektive Wahrnehmung. Dieses statische Bild der Raumzeit unterscheidet sich fundamental von unserem intuitiven Verständnis von Zeit als einer dynamischen Größe. (13)

Ganz anders als im Blogpost Gutsche 1, Das Rätsel der Zeit – Zeitfluss und Vergänglichkeit herausgearbeitet, „fließt“ Zeit in einem solchen Universum nicht. Vergangenheit und die Zukunft sind genauso real wie die Gegenwart – sie liegen nur an unterschiedlichen „Positionen“ in der Raumzeit. Das widerspricht unseren menschlichen Verständnis von Zeit als etwas, das fließt und bei der es einen fundamentalen Unterschied zwischen der Vergangenheit (als das, was unabänderbar vergangen ist), Gegenwart und Zukunft (als dem, was noch nicht ist) gibt.

 ×(4) Eine Weltlinie umfasst zum Beispiel alle Ereignisse, die eine Person von ihrer Geburt bis zu ihrem Tod erlebt – sozusagen die „Spur“ ihres Lebens in der Raumzeit. Eine ideale Weltlinie würde alle Ereignisse miteinander verbinden, die ein in Raum und Zeit besser lokalisierbares Objekt betreffen wie beispielsweise ein Atom. Aber hier stoßen wir an Grenzen der Lokalisierbarkeit durch die Heisenbergsche Unschärferelation und quantenphysikalische Effekte, die ich hier vorerst außer Acht lassen möchte.

In der folgenden Abbildung ist ein einfaches Beispiel einer Weltlinie dargestellt (grün). Ein Objekt, sagen wir: Annas Raumschiff, startet zum Zeitpunkt t=0 am Ort x=0 (das ist der Startplatz auf der Erde, die wir uns der Einfachheit halber uns als ruhend denken). Die Rakete bewegt sich dann mit konstanter Geschwindigkeit und befindet sich zur Zeit $t=t_A$ am Ort $x=x_A$.

Die Weltlinie, die die Rakete bis dahin durchläuft, ist die gerade Linie zwischen den Ereignissen 0 und A. Die Neigung der Linie visualisiert die Geschwindigkeit. Objekte mit senkrechter Weltlinie verbleiben am Ort 0. Man kann auch sagen: Solche Objekte bewegen sich ausschließlich in der Zeit weiter entlang der t-Achse. Wenn wir uns John als relativ faul denken, so können wir uns vorstellen, dass der sich vom Zeitpunkt 0 bis zum Zeitpunkt t=$t_A$ immer am selben Ort befindet (und dort seinen Kaffee trinkt).

Objekte mit waagerechter Weltlinie gibt es nicht, denn diese müssten ihre Raumkoordinate unendlich schnell ändern können. Das bringt uns zu einer Erweiterung des Raum-Zeit-Diagrammes.

Wie wir von der speziellen Relativitätstheorie wissen, kann sich im Raum nichts schneller als das Licht bewegen. Daher ist in unserem Diagramm auch die Weltlinie eines Photons – eines Lichtteilchens – eingezeichnet, das zur Zeit t=0 von der Erde in Richtung Sirius-System S ausgesendet wird (gelb). Es braucht 8.7 Jahre, um dorthin zu gelangen. Das heißt, das Photon erreicht einen 8.7 Lichtjahre entfernten Punkt ($x_S$) – das sind ungefähr 80 Billionen Kilometer – in 8.7 Jahren ($t_S$).

 ×(5) Streng genommen, zeigt das zweidimensionale Minkowski-Diagramm nur die Projektion eines Kegels. Lassen Sie mich das genauer erläutern. Alles, was sich mit Lichtgeschwindigkeit bewegt, liegt auf einer um 45° gegenüber der Zeitachse verkippten Geraden im Raum-Zeit-Diagramm. Weltlinien unterhalb dieser Geraden ($v > c$) sind unmöglich, da sich nichts schneller als das Licht bewegen kann. Daher sind bestimmte Bereiche des Raum-Zeit-Diagramms nicht kausal verbunden. Erweitert man ein Minkowski-Diagramm um eine zusätzliche Raumdimension (beispielsweise durch eine räumliche y-Achse, die senkrecht zur Bildebene orientiert ist), drehen sich die Geraden der Lichtstrahlen um die Zeitachse und bilden einen „Lichtkegel“. Daher dieser Begriff. In der vierdimensionalen Raumzeit kann dieser Lichtkegel nicht direkt dargestellt, jedoch gedacht werden.

Anmerkung zur besonderen Bedeutung der Zeitdimension: Im Kommentarbereich zum Blogpost Gutsche 1, Das Rätsel der Zeit – Zeitfluss und Vergänglichkeit hat @Fluffy allerdings zu Recht darauf hingewiesen, dass die Zeit, obgleich die physikalischen Gesetze der klassischen Physik symmetrisch in Bezug auf deren Richtung sind, als Koordinate durchaus einen ganz anderen Charakter als die drei räumlichen Koordinaten hat. In der Raumzeit kommt der Zeitachse daher sehr wohl eine besondere Bedeutung zu, denn diese bestimmt unter anderem die Lage des „Lichtkegels“, der kausal miteinander Bereiche definiert. Als Lichtkegel bezeichnet man den Bereich der Raumzeit, in dem sich Ereignisse befinden, die mit dem Ursprung eines Bezugssystems in kausaler Beziehung stehen können.

Die Zeitachse hat in der Raumzeit eine besondere Rolle, da sie die Lage des Lichtkegels bestimmt, der kausale Beziehungen definiert.

Die Kausalität in der Raumzeit wird durch Lichtkegel definiert, die Ereignisse in drei Kategorien einteilen:

• Zeitartig: Innerhalb des Kegels, kausal erreichbar durch physikalische Signale oder Bewegung.
• Lichtartig: Genau auf den Lichtkegeln, verbunden durch masselose Teilchen mit Lichtgeschwindigkeit.
• Raumartig: Außerhalb des Kegels, keine kausale Verbindung möglich.

 ×(11) Beachten Sie, dass im System mit den gestrichten Achsen „schiefwinkelige“ Koordinaten gebildet werden müssen.

Um die schiefwinkligen Koordinaten genauer zu verstehen, schauen wir uns die Punkte an, die auf den in der obigen Abbildung jeweils nummerierten Geraden liegen:

Die Gerade, die durch die mit dem blauen Punkt 1 markierte Strecke geht, verläuft parallel zur x-Achse. Alle Punkte auf dieser Geraden haben denselben ct-Wert (Zeitkoordinate im ersten Bezugssystem).

Die Gerade, die durch die mit dem blauen Punkt 2 markierte Strecke geht, verläuft parallel zur ct-Achse. Alle Punkte auf dieser Geraden haben denselben x-Wert (Ortskoordinate im ersten Bezugssystem).

Die Gerade, die durch die mit dem blauen Punkt 3 markierte Strecke geht, verläuft parallel zur x‘-Achse. Alle Punkte auf dieser Geraden haben denselben ct‘-Wert (Zeitkoordinate im zweiten Bezugssystem).

Die Gerade, die durch die mit dem blauen Punkt 4 markierte Strecke geht, verläuft parallel zur ct‘-Achse. Alle Punkte auf dieser Geraden haben denselben x‘-Wert (Ortskoordinate im zweiten Bezugssystem). Dies wird sehr schön hier visualisiert.